В.Я. Володин
РАСЧЁТ ДРОССЕЛЯ
Зачастую даже очень маститые разработчики электронной аппаратуры слабо разбираются в
электромагнитной технике и оказываются не в состоянии правильно выбрать конструкцию и
рассчитать электромагнитные компоненты ИВП. Порой доходит до смешного – разработчик
выбирает электромагнитные материалы того или иного производителя только потому, что
тот выкладывает для них, на своём сайте, бесплатное программное обеспечение, позволяющее
неспециалисту произвести оценочный расчёт типовых электромагнитных звеньев. Обычно, в
этом случае, результат далёк от совершенства. В этом нет ничего удивительного, т.к.
в наше время понятие электроника охватывает очень широкую область знаний и
специалист-разработчик, обычно получив образование в некой узкой области, на практике
порой вынужден принимать решения в смежных факультативных областях. Особенно остро эта
проблема касается любителей, которые вообще не имеют какого-то специального
образования.
Цель данной статьи, не выходя за пределы знаний полученных в объёме курса физики для
средней школы, дать упрощённую методику расчёта наиболее распространённого дросселя,
это дросселя работающего с подмагничиванием.
Чтобы полноценно использовать даже очень упрощённые расчётные формулы, нужно ясно
представлять их структуру. Поэтому будет полезно самостоятельно вывести те соотношения,
которые в дальнейшем нами будут использоваться.
Лично мне не нравится :), что обычно в классических источниках [1,2] по разному
оцениваются габариты магнитопровода для трансформаторов и дросселей. Для
трансформатора это Sc*So - произведение площади сечения сердечника Sc на площадь окна
с обмоткой So, а для дросселя объём сердечника Sc*lc – произведение сечения сердечника на
среднюю длину магнитной силовой линии. Обычно, дроссели, работающие с
подмагничиванием, имеют существенный немагнитный зазор, магнитное сопротивление
которого в сотни и тысячи раз больше магнитного сопротивления магнитопровода. Исходя
из этого, мы позволим себе игнорировать магнитное сопротивление сердечника, считая его
нулевым, и оценивать габариты дросселя так же как и габариты трансформатора, через
Sc*So.
И так, обмотка дросселя должна быть рассчитана на максимальный ток I протекающий через
неё. Зная максимальный ток I и плотность тока в обмотке J (в А/мм2), а так же площадь окна
магнитопровода So (в см2) и коэффициент его заполнения Ko, можно определить сколько
витков влезет в окно магнитопровода:
W=100*So*Ko*J/I (1)
Зная сечение магнитопровода Sc, а так же коэффициент его заполнения сталью Kc, можно,
для выбранной индукции B в магнитопроводе, определить потокосцепление обмотки
дросселя:
 Из (3) и (4) найдём индуктивность дросселя:
L=0,01*Sc*So*B*J*Kc*Ko/I^2 (5)
И величину Sc*So для сердечника дросселя:
Sc*So=100*L*I^2/(B*J*Kc*Ko) (6)
Для выбора значений B, J, Kc, Ko можно использовать аналогичные рекомендации для
трансформаторов [3]. При этом габаритную мощность Ргаб можно приравнять к Sc*So (Табл.1).
Для алюминиевого провода плотность тока следует уменьшить в 1.6 раз.
Из (3) и (4) найдём индуктивность дросселя:
L=0,01*Sc*So*B*J*Kc*Ko/I^2 (5)
И величину Sc*So для сердечника дросселя:
Sc*So=100*L*I^2/(B*J*Kc*Ko) (6)
Для выбора значений B, J, Kc, Ko можно использовать аналогичные рекомендации для
трансформаторов [3]. При этом габаритную мощность Ргаб можно приравнять к Sc*So (Табл.1).
Для алюминиевого провода плотность тока следует уменьшить в 1.6 раз.
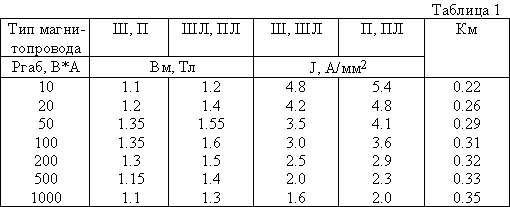 Таблица 1
Во избежание насыщения, магнитопровод дросселя должен иметь немагнитный зазор.
Считаем, что магнитопровод дросселя является идеальным магнитным проводником и все
ампервитки обмотки приложены к немагнитному зазору. Благодаря длинному немагнитному
зазору, индукция в магнитопроводе изменяется практически от нуля до Bm.
Длину немагнитного зазора (в мм), при известных ампервитках, можно определить по
формуле:
Таблица 1
Во избежание насыщения, магнитопровод дросселя должен иметь немагнитный зазор.
Считаем, что магнитопровод дросселя является идеальным магнитным проводником и все
ампервитки обмотки приложены к немагнитному зазору. Благодаря длинному немагнитному
зазору, индукция в магнитопроводе изменяется практически от нуля до Bm.
Длину немагнитного зазора (в мм), при известных ампервитках, можно определить по
формуле:
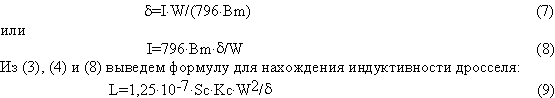 Обычно магнитопровод дросселя, работающего в режиме непрерывного тока, может
использоваться при более высокой частоте нежели это имело бы место в трансформаторе.
Всё дело в том, что при достаточно высокой средней индукции в сердечнике, изменение этой
индукции dB незначительно. Кратность увеличения частоты, при неизменных потерях,
можно определить по формуле [4]:
Po=Py*Gc*(dB/By)^2*(f/fy)^x,
Где: Po –потери в сердечнике;
Py – удельные потери для данного материала при заданных значениях амплитуды индукции
By и частоты fy синусоидальной магнитной индукции;
Gc – масса сердечника;
x – частотный показатель (1.2 - 1.8).
Отсюда, вероятно, кратность увеличения частоты - f/fy=(By/dB)^2/x. Т.е. при By/dB=10
железо, рассчитанное для работы на частоте 400Гц, будет вполне сносно себя вести на
частоте 10-20кГц.
Рассмотрим практические примеры:
Пример 1.
Допустим, мы строим регулируемый сварочный источник. Источник питается от однофазной
сети 220В 50Гц и регулировка сварочного тока в пределах от Iмин=50 до Iмакс=150А
осуществляется при помощи управляемого тиристорного выпрямителя, периодичность
нагрузки ПН=40%. Чтобы сварочная дуга не гасла в паузах напряжения дроссель, при
минимальном токе и максимальном угле регулирования, должен поддерживать ток на уровне
не ниже Iст=10А. Отсюда можно определиться с минимальной индуктивностью дросселя:
Lмин=0.25*Uд/(F*(Iмин-Iст))=0.25*(18+0.05*Iмин)/ (F*(Iмин-Iст))=
=0.25*(18+0.05*50)/(50*(50-10))=2.56мГн.
Дроссель будем мотать на Ш-образном сердечнике из стали 3411 (Э310). Предварительно
выберем B=1.3Тл, J=5А/мм^2 (с учётом заданной ПН), Ko=0.35, Kc=0.95. Отсюда по
формуле (6) найдём:
Sc*So=100*2.56e-3*150^2/(1.3*5*0.95*0.35)=2665см^4
Для дросселя надо использовать, как минимум, два сердечника ШЛ40х80 (Sc*Kc=30см^2,
So=40см^2).
Определим количество витков по формуле (1):
W=100*40*0.35*5/150=46 витков провода сечением Sпр=Iмакс/J=150/5=30мм^2
Определим немагнитный зазор по формуле (7):
Обычно магнитопровод дросселя, работающего в режиме непрерывного тока, может
использоваться при более высокой частоте нежели это имело бы место в трансформаторе.
Всё дело в том, что при достаточно высокой средней индукции в сердечнике, изменение этой
индукции dB незначительно. Кратность увеличения частоты, при неизменных потерях,
можно определить по формуле [4]:
Po=Py*Gc*(dB/By)^2*(f/fy)^x,
Где: Po –потери в сердечнике;
Py – удельные потери для данного материала при заданных значениях амплитуды индукции
By и частоты fy синусоидальной магнитной индукции;
Gc – масса сердечника;
x – частотный показатель (1.2 - 1.8).
Отсюда, вероятно, кратность увеличения частоты - f/fy=(By/dB)^2/x. Т.е. при By/dB=10
железо, рассчитанное для работы на частоте 400Гц, будет вполне сносно себя вести на
частоте 10-20кГц.
Рассмотрим практические примеры:
Пример 1.
Допустим, мы строим регулируемый сварочный источник. Источник питается от однофазной
сети 220В 50Гц и регулировка сварочного тока в пределах от Iмин=50 до Iмакс=150А
осуществляется при помощи управляемого тиристорного выпрямителя, периодичность
нагрузки ПН=40%. Чтобы сварочная дуга не гасла в паузах напряжения дроссель, при
минимальном токе и максимальном угле регулирования, должен поддерживать ток на уровне
не ниже Iст=10А. Отсюда можно определиться с минимальной индуктивностью дросселя:
Lмин=0.25*Uд/(F*(Iмин-Iст))=0.25*(18+0.05*Iмин)/ (F*(Iмин-Iст))=
=0.25*(18+0.05*50)/(50*(50-10))=2.56мГн.
Дроссель будем мотать на Ш-образном сердечнике из стали 3411 (Э310). Предварительно
выберем B=1.3Тл, J=5А/мм^2 (с учётом заданной ПН), Ko=0.35, Kc=0.95. Отсюда по
формуле (6) найдём:
Sc*So=100*2.56e-3*150^2/(1.3*5*0.95*0.35)=2665см^4
Для дросселя надо использовать, как минимум, два сердечника ШЛ40х80 (Sc*Kc=30см^2,
So=40см^2).
Определим количество витков по формуле (1):
W=100*40*0.35*5/150=46 витков провода сечением Sпр=Iмакс/J=150/5=30мм^2
Определим немагнитный зазор по формуле (7):
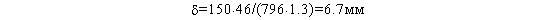 И, наконец, определим результирующую индуктивность по формуле (9):
L=1,25*10e-7*60*46^2/6.7=2.37мГн,
Что практически соответствует заданной минимальной индуктивности (на практике
индуктивность будет несколько выше, за счёт неучтённой индуктивности рассеяния).
Пример 2.
Как говорилось в первом примере, дроссель в основном нужен для поддержания тока в
паузах, вызванных работой выпрямителя (управляемого или не управляемого). В отсутствии
паузы в дросселе нет большой необходимости. Следовательно можно значительно уменьшить
габариты дросселя, если сделать его нелинейным, насыщающимся. Т.е. когда ток в дросселе
ниже тока насыщения Iнас, дроссель имеет значительную индуктивность, достаточную для
поддержания тока в паузах, а когда ток становится больше Iнас дроссель отключается,
т.к. его сердечник входит в насыщение. Применение подобного дросселя делает сварочный
ток импульсно модулированным. Модуляция возникает при насыщении дросселя и может даже
оказаться полезной, стимулируя капельный перенос металла с электрода в сварочную ванну.
Рассчитаем нелинейный дроссель, который работает при токе до Iнас=Iмин=50А. Чтобы
использовать наработанный ранее математический аппарат нам придётся немножко схитрить.
Дело в том, что при выводе формул мы считали, что дроссель работает в полном диапазоне
токов и, соответственно, максимальный сварочный ток соответствует току насыщения
сердечника дросселя. Поэтому, чтобы сохранить неизменным сечение провода, сделаем
плотность тока J в Iмакс/Iнас=150/50=3 раз меньше – J=5/3=1.67А/мм^2.
Посчитаем новое значение минимальной индуктивности дросселя:
Lмин=0.25*Uд/(F*(Iнас-Iст))=0.25*(18+0.05*50)/(50*(50-10))=2.56мГн
Дроссель так же будем мотать на Ш-образном сердечнике из стали 3411 (Э310). По формуле
(6) найдём:
Sc*So=100*L*Iнас^2/(B*J*Kc*Ko)=100*2.56e-3*50^2/(1.3*1.67*0.95*0.35)=886см^4,
что в три раза меньше результата полученного в предыдущем примере.
Для дросселя можно использовать один сердечник ШЛ40х64 (Sc*Kc=24см^2, So=40см^2).
Определим количество витков по формуле (1):
W=100*So*Ko*J/Iнас=100*40*0.35*1.67/50=46 витков провода сечением Sпр=Iнас/J=50/1.67=30мм^2
Как видно сечение провода не изменилось.
Определим немагнитный зазор по формуле (7):
И, наконец, определим результирующую индуктивность по формуле (9):
L=1,25*10e-7*60*46^2/6.7=2.37мГн,
Что практически соответствует заданной минимальной индуктивности (на практике
индуктивность будет несколько выше, за счёт неучтённой индуктивности рассеяния).
Пример 2.
Как говорилось в первом примере, дроссель в основном нужен для поддержания тока в
паузах, вызванных работой выпрямителя (управляемого или не управляемого). В отсутствии
паузы в дросселе нет большой необходимости. Следовательно можно значительно уменьшить
габариты дросселя, если сделать его нелинейным, насыщающимся. Т.е. когда ток в дросселе
ниже тока насыщения Iнас, дроссель имеет значительную индуктивность, достаточную для
поддержания тока в паузах, а когда ток становится больше Iнас дроссель отключается,
т.к. его сердечник входит в насыщение. Применение подобного дросселя делает сварочный
ток импульсно модулированным. Модуляция возникает при насыщении дросселя и может даже
оказаться полезной, стимулируя капельный перенос металла с электрода в сварочную ванну.
Рассчитаем нелинейный дроссель, который работает при токе до Iнас=Iмин=50А. Чтобы
использовать наработанный ранее математический аппарат нам придётся немножко схитрить.
Дело в том, что при выводе формул мы считали, что дроссель работает в полном диапазоне
токов и, соответственно, максимальный сварочный ток соответствует току насыщения
сердечника дросселя. Поэтому, чтобы сохранить неизменным сечение провода, сделаем
плотность тока J в Iмакс/Iнас=150/50=3 раз меньше – J=5/3=1.67А/мм^2.
Посчитаем новое значение минимальной индуктивности дросселя:
Lмин=0.25*Uд/(F*(Iнас-Iст))=0.25*(18+0.05*50)/(50*(50-10))=2.56мГн
Дроссель так же будем мотать на Ш-образном сердечнике из стали 3411 (Э310). По формуле
(6) найдём:
Sc*So=100*L*Iнас^2/(B*J*Kc*Ko)=100*2.56e-3*50^2/(1.3*1.67*0.95*0.35)=886см^4,
что в три раза меньше результата полученного в предыдущем примере.
Для дросселя можно использовать один сердечник ШЛ40х64 (Sc*Kc=24см^2, So=40см^2).
Определим количество витков по формуле (1):
W=100*So*Ko*J/Iнас=100*40*0.35*1.67/50=46 витков провода сечением Sпр=Iнас/J=50/1.67=30мм^2
Как видно сечение провода не изменилось.
Определим немагнитный зазор по формуле (7):
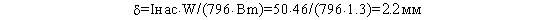 И, наконец, определим результирующую индуктивность по формуле (9):
L=1,25*10e-7*24*46^2/2.2=2.88мГн,
Как говорится, комментарии излишни!
Литература:
1.Под ред. Г.С. Найвелта. Справочник: Источники электропитания радиоэлектронной
аппаратуры. М.: Радио и Связь, 1986 год, стр.116-121.
2. К.Б. Мазель. Выпрямители и стабилизаторы напряжения. М-Л.: Госэнергоиздат, 1951 год,
стр.55-60.
3. С.Г. Бунин, Л.П.Яйленко. Справочник радиолюбителя - коротковолновика.
К.: Технiка, 1984 год, стр.203-204.
4. В.В. Губанов. Стабилизированные полупроводниковые преобразователи в системе с
нелинейными резонансными устройствами. Л.: Знергоатомиздат, 1985 год, стр.12.
И, наконец, определим результирующую индуктивность по формуле (9):
L=1,25*10e-7*24*46^2/2.2=2.88мГн,
Как говорится, комментарии излишни!
Литература:
1.Под ред. Г.С. Найвелта. Справочник: Источники электропитания радиоэлектронной
аппаратуры. М.: Радио и Связь, 1986 год, стр.116-121.
2. К.Б. Мазель. Выпрямители и стабилизаторы напряжения. М-Л.: Госэнергоиздат, 1951 год,
стр.55-60.
3. С.Г. Бунин, Л.П.Яйленко. Справочник радиолюбителя - коротковолновика.
К.: Технiка, 1984 год, стр.203-204.
4. В.В. Губанов. Стабилизированные полупроводниковые преобразователи в системе с
нелинейными резонансными устройствами. Л.: Знергоатомиздат, 1985 год, стр.12.